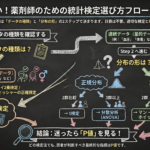
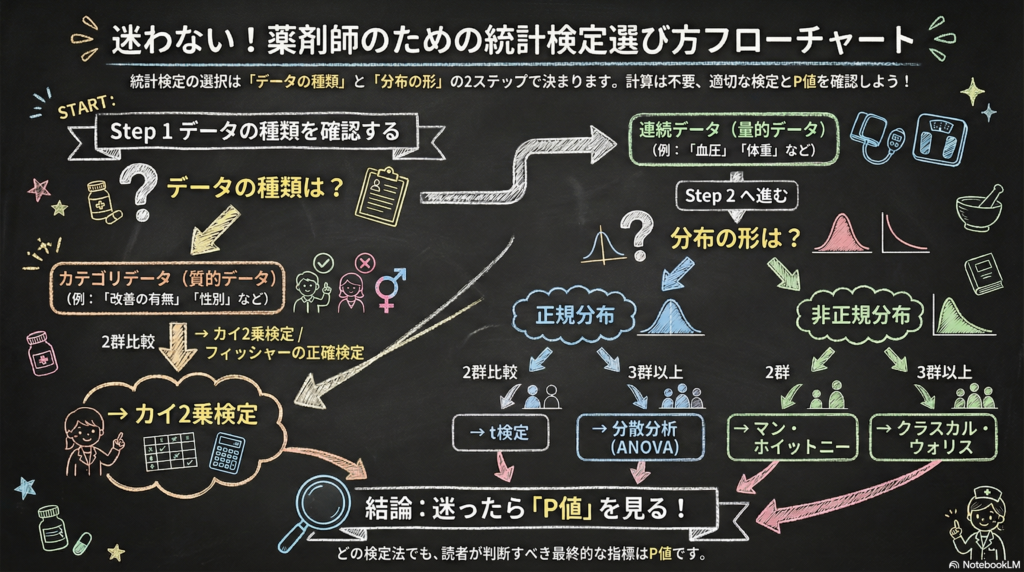
「t検定とWilcoxonの順位和検定、どっちを使えばいいんですか?」「カイ二乗検定とFisherの直接確率法、違いは何ですか?」。論文のMethodsを読むとき、こうした検定法の名前が出てきて混乱することはありませんか。
この記事では、よく使われる検定法の選び方を、データのタイプと分布に応じて整理します。難しい数式は不要です。「この状況ではこの検定法」という対応関係を押さえることが目的です。
目次
検定法を選ぶ前に ― データのタイプを確認する
検定法を選ぶ第一歩は、扱っているデータがどのタイプかを確認することです。
| データタイプ | 説明 | 例 |
|---|---|---|
| 連続変数 | 数値で表され、大小関係と間隔が意味を持つ | 年齢、血圧、HbA1c |
| カテゴリー変数 | グループに分類される | 性別、有病・無病、治療群・対照群 |
| 順序変数 | 順序はあるが、間隔が等しくない | 痛みの程度(軽い・中程度・強い) |
データタイプって、そんなに重要なんですか?

オカメインコさん

ポッポ先生
非常に重要です。データタイプに合わない検定法を使うと、誤った結論になる可能性があります。ここは押さえたいですね
連続変数の検定法
2群の比較
| 状況 | 検定法 | 特徴 |
|---|---|---|
| 正規分布、分散が等しい | Studentのt検定 | 最も一般的。検定力が高い |
| 正規分布、分散が異なる | Welchのt検定 | 分散の異なる群でも使える |
| 正規分布でない、または外れ値がある | Mann-WhitneyのU検定(Wilcoxonの順位和検定) | 非参数検定。分布を仮定しない |
3群以上の比較
| 状況 | 検定法 | 特徴 |
|---|---|---|
| 正規分布、分散が等しい | 一元配置分散分析(ANOVA) | 3群以上の平均値の比較 |
| 正規分布でない、または外れ値がある | Kruskal-Wallis検定 | 非参数検定 |
対応のあるデータ(同じ対象の前後比較)
| 状況 | 検定法 | 特徴 |
|---|---|---|
| 正規分布 | 対応のあるt検定(paired t-test) | 同じ対象の前後比較 |
| 正規分布でない | Wilcoxonの符号付順位検定 | 非参数検定 |
カテゴリー変数の検定法
2×2の分割表(2群×2カテゴリー)
| 状況 | 検定法 | 特徴 |
|---|---|---|
| 期待度数が5以上のセルが80%以上 | カイ二乗検定 | 最も一般的 |
| 期待度数が小さいセルがある | Fisherの直接確率法 | 小サンプルでも正確 |
カイ二乗検定とFisherの検定、どっちを使えばいいんですか?

オカメインコさん

ポッポ先生
サンプルサイズが大きく、各セルの期待度数が5以上ならカイ二乗検定。小さい場合はFisherの検定が適切です。論文ではFisherの検定を使っている場合、サンプルサイズが小さいことを示唆しています
2×kの分割表(2群×kカテゴリー)
- カイ二乗検定:3群以上の比率の比較
検定法選択のまとめ表
| データタイプ | 群数 | 分布 | 検定法 |
|---|---|---|---|
| 連続変数 | 2群(独立) | 正規分布 | Studentのt検定 |
| 連続変数 | 2群(独立) | 非正規分布 | Mann-WhitneyのU検定 |
| 連続変数 | 2群(対応あり) | 正規分布 | 対応のあるt検定 |
| 連続変数 | 2群(対応あり) | 非正規分布 | Wilcoxonの符号付順位検定 |
| 連続変数 | 3群以上 | 正規分布 | ANOVA |
| カテゴリー変数 | 2群 | – | カイ二乗検定 or Fisherの検定 |
まとめ
- データタイプ(連続・カテゴリー)を確認する
- 群数(2群か3群以上か)を確認する
- 対応があるか(同じ対象の前後比較か)を確認する
- 正規分布かどうかを確認する
- 論文のMethodsで使われている検定法を確認する
次に論文のMethodsを読むとき、どの検定法が使われているか確認する習慣をつけてみてください。